《复杂度分析与流程图》

算法的定义与特征

程序=算法+数据结构，其中算法可以理解为解决实际问题的方法，数据结构则是计算机存储、组织数据的方式。

算法是程序设计的核心和灵魂，有了算法就可以结合数据结构转变成程序。

编程解决问题的流程图：

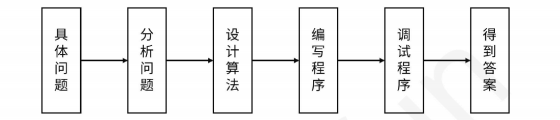
算法就是解决问题的操作步骤。一个算法必须满足以下五个重要的特征：

1. 有穷性：执行有穷步、在有穷的时间内完成。
2. 确切性：每一条指令必须有确切的含义，不会产生歧义。在任何条件下算法只有唯一的一条执行路径。
3. 可行性：算法中的操作可以通过执行有限次来实现。
4. 输入：一个算法有零个或者多个输入。
5. 输出：一个算法有一个或者多个输出。

---

时间复杂度

问题规模与语句频度

算法效率从以下两个方面考虑：

1. 时间效率：指算法所耗费的时间；
2. 空间效率：指算法执行过程中所耗费的存储空间。
   （时间效率和空间效率有时是矛盾的）

算法时间效率度量方式：

1. 事后统计：将算法实现，测算其时间和空间开销；
   缺点：编写程序实现算法花费较多时间和精力；实验结果依赖计算机软硬件环境。
2. 事前统计：对算法所消耗资源的预估方法。

算法运行时间 = 一个简单操作所需时间 × 简单操作次数
即算法中每条语句的执行时间之和：

$$\text{算法运行时间} = \sum (\text{每条语句执行次数} \times \text{该语句执行一次所需时间}) $$

计算机性能等硬件因素与算法无关，默认为单位时间1：

$$\text{算法运行时间} = \sum \text{每条语句频度}$$

例：画边长为n个*号的正方形代码时间复杂度为：

$$T(n) = f(n) = 2n^2 + 2n$$

---

时间复杂度概念

为比较算法效率，仅比较数量级（如 $f_1=10n^2$ 与 $f_2=5n^3$，当 $n$ 足够大时 $f_1$ 更优）。
若存在辅助函数 $f(n)$，使得当 $n \to \infty$ 时 $T(n)/f(n)$ 的极限值为非零常数，则称 $f(n)$ 是 $T(n)$ 的同数量级函数，记作 $T(n) = O(f(n))$，称为渐进时间复杂度（简称时间复杂度）。

例：画正方形算法耗费时间 $f(n) = n^2 + 3n$，

当 $n \to \infty$ 时 $f(n)/n^2 \to 1$，时间复杂度为 $O(n^2)$。

---

最好、最坏和平均时间复杂度

• 最坏时间复杂度：最坏情况下算法的时间复杂度。
• 平均时间复杂度：所有可能输入实例等概率出现时算法的期望运行时间。
• 最好时间复杂度：最好情况下算法的时间复杂度。
  一般优先考虑最坏时间复杂度以保证算法稳定性。

---

时间复杂度计算

复杂算法中，用基本语句度量工作量（基本语句特点）：

1. 重复次数与执行时间成正比
2. 对运行时间贡献最大
3. 执行次数最多

计算步骤：

1. 找到执行次数最多的语句作为基本语句
2. 计算基本语句执行数量级 $f(n)$
3. 用 $O(f(n))$ 表示结果

常见时间复杂度对比：

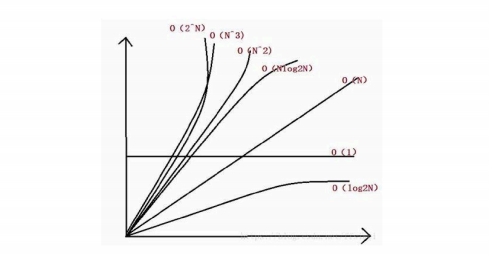
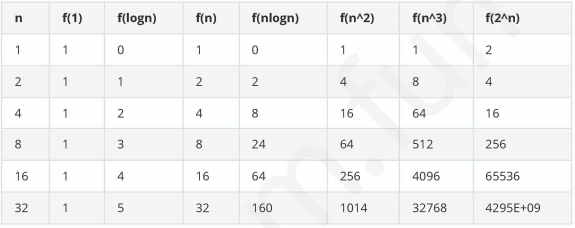
复杂度由低到高排序：

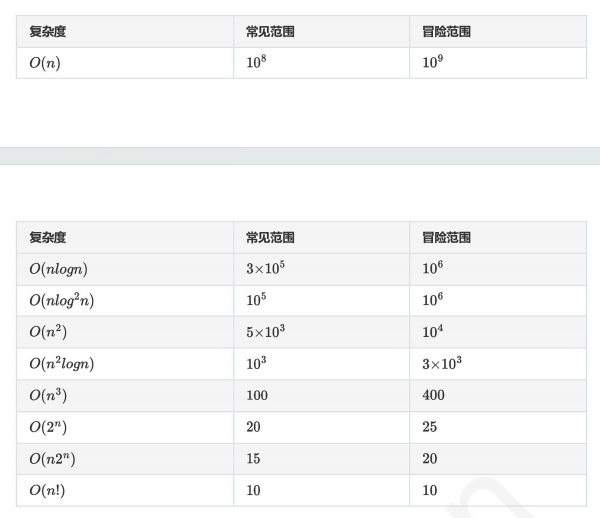
时间复杂度实用范围：

---

样例分析

1. $O(1)$

   x++;
   s = 0;
   

2. $O(n)$

   for (int i = 1; i <= n; i++) {
       s += i;  // 基本语句执行n次
   }
   

3. $O(n)$（递归阶乘）

   long long f(int n) {
       if (n == 0) return 1;
       return f(n - 1) * n;  // 调用n次
   }
   

4. $O(n^2)$

   int x = 0, y = 0;
   for (int k = 1; k <= n; k++) { x++; }          // n次
   for (int i = 1; i <= n; i++) {
       for (int j = 1; j <= n; j++) { y++; }      // n²次
   }
   

5. $O(n \times m)$

   for (int i = 1; i <= m; i++) {
       for (int j = 1; j <= n; j++) { s += a[i][j]; }  // m×n次
   }
   

6. $O(n^3)$

   int x = 1;
   for (int i = 1; i <= n; i++) {
       for (int j = 1; j <= n; j++) {
           for (int k = 1; k <= n; k++) { x++; }  // n³次
       }
   }
   

7. $O(n^3)$（三重循环累加）

   int x = 1;
   for (int i = 1; i <= n; i++) {
       for (int j = 1; j <= i; j++) {
           for (int k = 1; k <= j; k++) { x++; }  // ∑∑∑ = n(n+1)(n+2)/6
       }
   }
   

8. $O(\log n)$

   i = 1;
   while (i <= n) { i *= 2; }  // 执行次数 ≤ log₂n
   

9. $O(n \log n)$

   x = 0;
   for (int i = 1; i <= n; i *= 2) {    // O(log n) 
       for (int j = 1; j <= n; j++) {   // O(n)
           x++;
       }
   }
   

10. $O(2^n)$（斐波那契递归）

    int fibonacci(int n) {
        if (n <= 1) return n;
        return fibonacci(n - 1) + fibonacci(n - 2);  // 指数级调用
    }
    

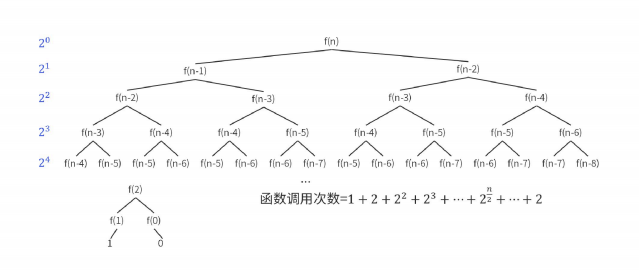
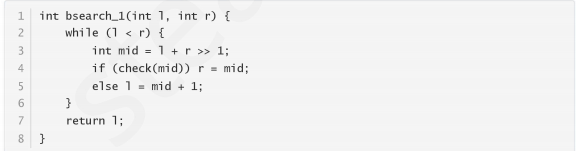
11. $O(\log n)$（二分查找）

---

空间复杂度

概念

空间复杂度：算法所需存储空间的度量，记作 $S(n) = O(f(n))$，其中 $n$ 为问题规模。
算法占据空间包括：

• 算法本身占用空间（指令、常数等）
• 辅助空间（额外申请的内存）

例：数组逆序存放

• 算法1（空间复杂度 $O(1)$）：

  for (int i = 0; i < n / 2; i++) {
      int t = a[i];
      a[i] = a[n - i - 1];
      a[n - i - 1] = t;
  }
  

• 算法2（空间复杂度 $O(n)$）：

  int b[n];
  for (int i = 0; i < n; i++) { b[i] = a[n - i - 1]; }
  for (int i = 0; i < n; i++) { a[i] = b[i]; }
  

---

内存限制问题

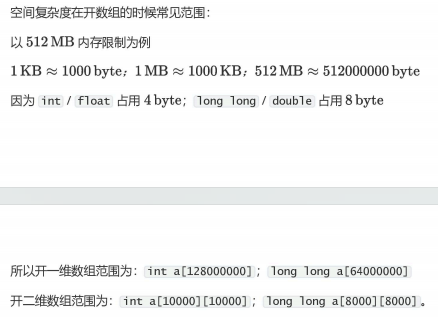
信息学奥赛中内存限制通常为 512MB：

• 1 KB ≈ 1000 byte
• 1 MB ≈ 1000 KB → 512 MB ≈ 512,000,000 byte
• int / float：4 byte
• long long / double：8 byte

可开数组范围：

---

流程图应用

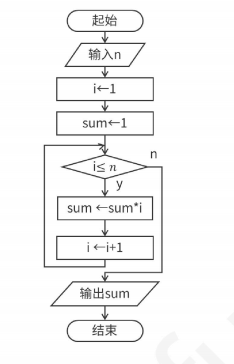
例1：求阶乘流程图

int factorial(int n) {
    int f = 1;
    for (int i = 1; i <= n; i++) {
        f = f * i;
    }
    return f;
}

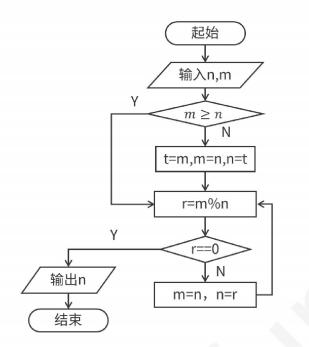
例2：辗转相除法求最大公约数（输入 n=6, m=28，输出结果=2）

int gcd(int a, int b) {
    while (b != 0) {
        int r = a % b;
        a = b;
        b = r;
    }
    return a;
}

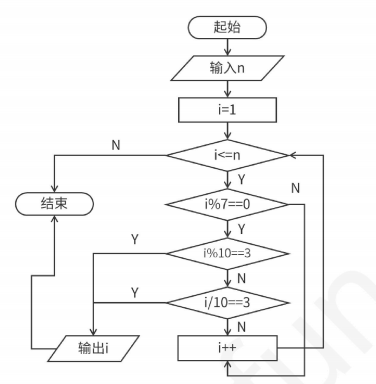
例3：找出小于n且满足条件的数（能被7整除且个位或十位含3）

for (int i = 1; i < n; i++) {
    if (i % 7 == 0 && (i % 10 == 3 || i / 10 % 10 == 3)) {
        cout << i << endl;
    }
}

---

伪代码

伪代码：用自然语言（中/英文）编写的算法描述，不受编程语言语法限制。
优点：

• 提高算法可读性
• 架起程序与算法/流程图之间的桥梁
• 简化文档编写

编写标准：

1. 按任务序列组织伪代码
2. 以伪代码声明开头，明确主要目标
3. 用缩进代替 begin-end
4. 循环语句支持 while、repeat-until、for
5. 变量不需声明，局部于特定过程
6. 赋值用 ← 表示（如 x ← y）
7. 注释符号用 △
8. 保持完整性和可理解性

示例：

Begin
    Input x, y     △ 输入x=5, y=8
    A ← x          △ A=5
    x ← y          △ x=8
    y ← A          △ y=5
    Print x, y     △ 输出8,5
End

---

例题

[CSP-J 2020] 冒泡排序伪代码：

FLAG ← n
while FLAG > 1 do
    k ← FLAG - 1
    FLAG ← 1
    for j = 1 to k do
        if L[j] > L[j+1] then
            swap(L[j], L[j+1])
            FLAG ← j

问题：对n个数用此算法排序，最少需比较多少次？
解析：当数组已有序时，第一轮循环比较n-1次后终止。答案为 C. n-1。