一、单项选择题（共 15 题，每题 2 分，共计 30 分；每题有且仅有一个正确选项）

1. 十进制整数 $-5$ 的 $8$ 位二进制补码为？

{{ select(1) }}

• 11111101

• 11111010

• 10000101

• 11111011

2. 用数字 1,2,3,4,5 组成无重复数字的 $5$ 位数，要求： ① 万位为奇数； ② 千位数字比十位数字大； ③ 个位不为 $2$。

这样的 $5$ 位数共有（）种。

{{ select(2) }}

• $27$

• $36$

• $54$

• $84$

3. 中缀表达式 a + b * (c - d) / e 对应的后缀表达式为？

{{ select(3) }}

• a b c d - * e / +

• a b c d * - e / +

• a b c - d * e / +

• a b c d - * / e +

4. 递归函数 fact 计算阶乘，代码如下，执行 fact(3) 时，函数调用栈的入栈顺序（从栈底到栈顶）为？

int fact(int n) {
    if (n == 1) return 1;
    return n * fact(n-1);
}

{{ select(4) }}

• fact(3) → fact(2) → fact(1)

• fact(1) → fact(2) → fact(3)

• fact(3) → fact(2) → fact(1) → fact(2) → fact(3)

• fact(1) → fact(2) → fact(3) → fact(2) → fact(1)

5. 下列哪个表达式可正确判断非负整数 $n$ 是 “$2$ 的正整数次幂”（如 $2$、$4$、$8$...）？

{{ select(5) }}

• (n | (n - 1)) == -1

• (n > 0) && (n ^ (n - 1)) == 2 * n - 1

• (n & (n - 1)) == 0

• (n > 1) && ((n & (n - 1)) == 0)

6. 64 位系统下，int arr[3][4]; 与 int *ptr[3]; 占用内存之和为？

{{ select(6) }}

• $48$ 字节
• $60$ 字节
• $72$ 字节
• $120$ 字节

7. 判断单链表是否有环，下列方法错误的是？

{{ select(7) }}

• 存储每个节点的地址，在遍历过程中，若发现当前节点的地址已经被存储过，则说明有环。

• 用快慢指针同时从 head 出发遍历链表（快指针每次 2 步，慢指针每次 1 步），若相遇则有环

• 遍历链表时给节点加 “访问标记”，若再次遇到标记节点则有环

• 遍历至尾节点，若尾节点 next 指向表头则有环

8. 有序数组 a = [82, 85, 88, 90, 93, 96]，用二分法查找 “第一个大于 $91$ 的元素”，若使用如下代码模板，下列 ①②③④ 应填入？

int left = 0, right = 5;
while (①) {
	int mid = (left + right) / 2;
	if (a[mid] <= 91) 
	{
		②
	}
    else if (a[mid] > 91) 
	{
		③
	}
}
④

{{ select(8) }}

• ① left < right ② left = mid + 1; ③ right = mid - 1; ④ cout << a[left];

• ① left < right ② left = mid + 1; ③ right = mid; ④ cout << a[right];

• ① left <= right ② left = mid + 1; ③ right = mid - 1; ④ cout << a[right];

• ① left <= right ② left = mid + 1; ③ right = mid; ④ cout << a[left];

9. 执行下列代码后，$x$ 和 $y$ 的值分别为？

int x = 10, y = 20;
int *ptr = &x; 
ptr = &y;      
int &ref = x;  
ref = y;        

{{ select(9) }}

• x=10, y=20

• x=20, y=20

• x=10, y=10

• x=20, y=10

10. 有 $n$ 级台阶，每次可跨 $1$ 级或 $2$ 级，但不能连续跨 $2$ 级（即跨 $2$ 级后必须跨 $1$ 级）。 $f(n)$ 表示到达第 $n$ 级台阶的方案数，则关于 $f(n)$ 说法正确的是（）

{{ select(10) }}

• 等于斐波那契数列第 $n$ 项

• 递推公式为 f(n) = f(n-1) + f(n-2) + f(n-3) ($n \geq 3$)

• 递推公式为 f(n) = f(n-1) + f(n-3) ($n \geq 3$)

• 递推公式为 f(n) = f(n-2) + f(n-3) ($n \geq 3$)

11. 已知某二叉树的前序遍历序列为 ABDCFGE，中序遍历序列为 DBAFCGE，则其后续遍历序列是（）

{{ select(11) }}

• DBFEGCA

• DBFGEAC

• DBEFGCA

• DBFEGAC

12. 已知有向无环图（DAG）的节点为 1~8，有以下有向边：1→2，1→3，2→4，2→5，3→5，3→6，4→7，5→7，5→8，6→8，7→8。下列选项中，不可能是该图拓扑排序的是（）

{{ select(12) }}

• 1,2,3,4,5,6,7,8

• 1,2,3,6,5,4,8,7

• 1,3,2,5,4,7,6,8

• 1,3,2,5,6,4,7,8

13. 某班有 $8$ 名男生和 $6$ 名女生，从中选出 $3$ 人参加竞赛，要求至少有 $1$ 名男生和 $1$ 名女生，且男生甲和女生乙不能同时入选，则不同的选法有（）种。

{{ select(13) }}

• $252$

• $274$

• $276$

• $288$

14. 某老师课间答疑时间为 $1$ 小时（$0\sim 60$ 分钟），有 $5$ 名学生申请答疑，时间区间（开始分钟，结束分钟）如下：[(5,15), (10,25), (20,35), (30,45), (40,55)]。老师每次只能给一个同学答疑，最多可答疑多少人？

{{ select(14) }}

• $2$
• $3$
• $4$
• $5$

15. $3$ 个相同节点构成的二叉树的形态共有（）种？（提示：根-左儿子和根-右儿子属于不同的形态，根-左儿子和根-左儿子属于相同形态）

{{ select(15) }}

• $4$
• $5$
• $6$
• $7$

二、阅读程序（程序输入不超过数组或字符串定义的范围；判断题选正误；除特殊说明外，判断题每题2分，选择题每题3分，共40分）

（一）阅读下列程序，回答问题。

注意：数据保证，输入的字符串的两个字符串仅包含大小写字母。

假设第一个字符串的长度为 $n$，第二个字符串的长度为 $m$，保证 $2 \leq n < 100$，$1 \leq m < 10^5$

判断题

16. 如果输入的第一个字符串长度等于 $100$，程序可能达不到原本的目的。 {{ select(16) }}

• 正确

• 错误

17. 输出结果可能为 $m$ （即第二个字符串的长度）。 {{ select(17) }}

• 正确

• 错误

18. 可以将代码 ① 中的 32 替换为 'A' - 'a'，输出结果不会改变。 {{ select(18) }}

• 正确

• 错误

选择题

19. 若输入的两个字符串分别为 Aba 和 aBababcAba，答案为（） {{ select(19) }}

• $1$

• $2$

• $3$

• $4$

20. （4分）若输入的第一个字符串为 $cbc$，第二个字符串的长度为 $6$，且均为小写字母，最后输出结果为 $2$，则第二个字符串可能的输入有多少种 () {{ select(20) }}

• $26$

• $27$

• $52$

• $53$

（二）阅读下列程序，回答问题。

保证 $1\le n \le 10^5$，$-10^{10} \le a[i] \le 10^{10}$；

$-10^5 \le s,d \le 10^5$，$1\le l\le r \le n$。

判断题

21. 当 l == r，输出数组和原数组相同。{{ select(21) }}

• 正确
• 错误

22. 当 s == 0 时，$a[l]$ 的值一定不会改变。{{ select(22) }}

• 正确
• 错误

23. 一定存在一种合法的输入，使得最终输出的数和原数组中的数相同。 {{ select(23) }}

• 正确
• 错误

选择题

24. 对于以下输入，输出结果为（）

5 
2 2 3 4 5
4 5 2 3

{{ select(24) }}

• 2 2 3 6 10
• 2 2 3 9 13
• 2 2 3 7 10
• 2 2 5 9 13

25. （4分）关于该程序说法正确的是 () {{ select(25) }}

• 该程序的时间复杂度为 $O(n^2)$
• 该程序是可以实现，将一个序列中的某个区间加上一个等差数列。
• 该程序一定不能实现，将一个序列中的某个区间加上或减去一个数。
• 输出后的值一定大于等于原数组中的对应值。

（三）阅读下列程序，回答问题。

保证输入的字符串长度不超过 $1000$，且仅包含大写字母。

判断题

26. 当字符串长度为 $1$ 时，输入的字符不同，输出的结果也不同。（）{{ select(26) }}

• 正确

• 错误

27. 将代码二中的 i <= 'Z' 修改为 i <= 'z' 后，该程序可以处理包含大小写字母的输入。{{ select(27) }}

• 正确

• 错误

28. 删去代码三的内容，不会影响程序的输出结果。 {{ select(28) }}

• 正确

• 错误

选择题

29. （4分）若输入的字符串为非法字符串 $AABBCcCD$，输出结果为： {{ select(29) }}

• 1111111010000110
• 11111010010100
• 01011010111100
• 10101111010100

30. （4分）关于该程序，说法错误的是（） {{ select(30) }}

• 将代码一修改为 Code[root->ch] = code; 一定会影响程序输出结果。
• pq 内部的排序方式为：先按频率排序，再按字符排序，频率越低的，越先出队，如果频率相同，字符越小的，越先出队。
• 程序实现了对输入字符串的编码，对于每一个字符所对应的编码，一定不会出现，一个字符的编码是另一个字符的编码的前缀的情况。
• 程序实现了对输入字符串的编码，这是一种平均长度最短的无损编码方式。

三、完善程序（单选题，每小题3分，共计30分）

（一）完善程序第一题

输入两个较大的正整数 $num1,num2$，求 $num1/num2$ 的商和余数。

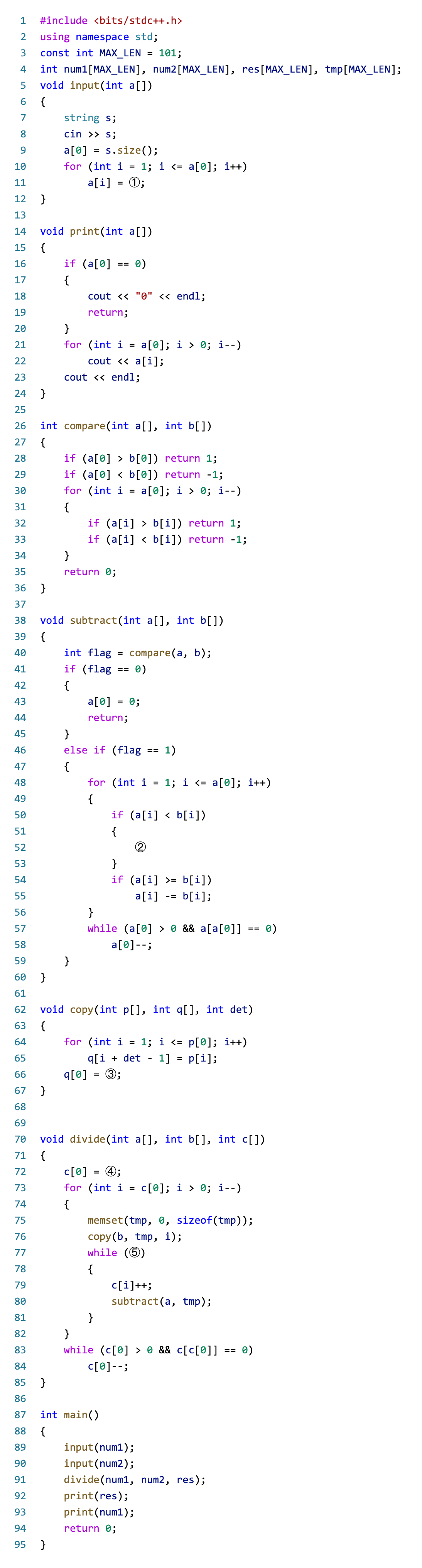
31. ①处应填入（） {{ select(31) }}

• s[i] - '0'
• s[i + 1] - '0'
• s[a[0] - i + 1] - '0'
• s[a[0] - i] - '0'

32. ②处应填入（） {{ select(32) }}

• a[i - 1] += 10; a[i]--;
• a[i + 1]--; a[i] += 10;
• b[i - 1]--; b[i] += 10;
• b[i] -= 10; b[i + 1]++;

33. ③处应填入（） {{ select(33) }}

• p[0] + det - 1
• p[0] + det + 1
• p[0] + det;
• p[0]

34. ④处应填入（） {{ select(34) }}

• a[0] + b[0] - 1
• a[0] + b[0]
• a[0] - b[0] + 1
• a[0] - b[0]

35. ⑤处应填入（）{{ select(35) }}

• compare(a, tmp)
• compare(a, tmp) > 0
• compare(a, tmp) >= 0
• compare(a, tmp) != 1

（二）完善程序第二题

给定 $n$ 个点和 $m$ 条边，每条边都有一定的长度。

现在从一号点出发，到达点 $T$，寻找路径上经过边的数量小于等于 $K$ 的路径，求出所有满足条件的路径中最长边长度的最小值。

36. ①处应填入（） {{ select(36) }}

• memset(head, -1, sizeof(head));
• memset(head, 0, sizeof(head));
• memset(head, -1, sizeof(-1));
• memset(head, -1, sizeof(0));

37. ②处应填入（） {{ select(37) }}

• q.push({1, -1});
• q.push({1, 0});
• q.push({T, -1});
• q.push({T, 0});

38. ③处应填入（） {{ select(38) }}

• int i = head[u]; i; i = E[i].next
• int i = head[u]; i; i = E[u].next
• int i = head[u]; ~i; i = E[i].next
• int i = head[u]; ~i; i = E[u].next

39. ④处应填入（） {{ select(39) }}

• !vis[v] && E[i].dist <= max_d && step <= K
• !vis[v] && E[i].dist < max_d && step <= K
• !vis[v] && E[i].dist < max_d && step < K
• !vis[v] && E[i].dist <= max_d && step < K

40. ⑤处应分别填入（） {{ select(40) }}

• right = mid; left = mid;
• right = mid - 1; left = mid;
• right = mid; left = mid + 1;
• right = mid - 1; left = mid + 1;