登录以参加训练计划

以下是针对 CSP-J 进制转换算法 的详细解析与代码实现，帮助您系统掌握相关知识点：

---

一、进制转换基础

1. 进制定义

• 十进制（Decimal）：基数为10，数字范围 0-9。
• 二进制（Binary）：基数为2，数字范围 0-1。
• 八进制（Octal）：基数为8，数字范围 0-7。
• 十六进制（Hexadecimal）：基数为16，数字范围 0-9, A-F（或 a-f）。

2. 进制转换方法

(1) 十进制转其他进制（除基取余法）

步骤：

1. 用十进制数除以目标基数，记录余数。
2. 将商继续除以基数，直到商为0。
3. 余数按逆序排列即为目标进制数。

示例：十进制数 13 转二进制

13 ÷ 2 = 6 ... 1  
6 ÷ 2 = 3 ... 0  
3 ÷ 2 = 1 ... 1  
1 ÷ 2 = 0 ... 1  
结果：1101

(2) 其他进制转十进制（按权展开法）

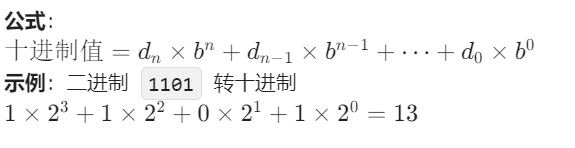
(3) 二进制与十六进制互转

• 二进制 → 十六进制：每4位二进制对应1位十六进制（不足补0）。
  1101 1010 → DA
• 十六进制 → 二进制：每位十六进制展开为4位二进制。
  E → 1110

---

二、编程实现

1. 十进制转二进制（C++）

#include <iostream>
#include <string>
using namespace std;

string decimalToBinary(int n) {
    if (n == 0) return "0";
    string bin;
    while (n > 0) {
        bin = to_string(n % 2) + bin; // 逆序拼接
        n /= 2;
    }
    return bin;
}

int main() {
    int num;
    cin >> num;
    cout << decimalToBinary(num);
    return 0;
}

2. 二进制转十进制（C++）

#include <iostream>
using namespace std;

int binaryToDecimal(string bin) {
    int dec = 0, base = 1;
    for (int i = bin.size()-1; i >= 0; i--) {
        dec += (bin[i] - '0') * base;
        base *= 2;
    }
    return dec;
}

int main() {
    string bin;
    cin >> bin;
    cout << binaryToDecimal(bin);
    return 0;
}

3. 十六进制转十进制（处理字母）

#include <iostream>
using namespace std;

int hexToDecimal(string hex) {
    int dec = 0, base = 1;
    for (int i = hex.size()-1; i >= 0; i--) {
        char c = hex[i];
        int val = (c >= '0' && c <= '9') ? c - '0' 
                 : (toupper(c) - 'A' + 10); // 处理A-F
        dec += val * base;
        base *= 16;
    }
    return dec;
}

int main() {
    string hex;
    cin >> hex;
    cout << hexToDecimal(hex);
    return 0;
}

---

三、C++库函数辅助转换

1. 字符串转数值（支持进制）

#include <string>
using namespace std;

int main() {
    string binary = "1101";
    int num = stoi(binary, nullptr, 2); // 二进制转十进制 → 13
    
    string hex = "1A";
    int num2 = stoi(hex, nullptr, 16); // 十六进制转十进制 → 26
}

2. 数值转字符串（指定进制输出）

#include <bitset>
#include <sstream>

int main() {
    int num = 13;
    
    // 转二进制字符串
    string bin = bitset<8>(num).to_string(); // 00001101
    
    // 转十六进制字符串
    stringstream ss;
    ss << hex << num; // d
    string hex = ss.str();
}

---

四、常见题型与技巧

1. 补码与负数处理

• 负数的二进制表示：计算机中使用补码。
  -5 的8位二进制补码：
  原码 → 10000101 → 反码11111010 → 补码11111011

2. 大数处理（高精度转换）

当数值超过 long long 范围时，需用字符串模拟计算：

string decimalToBase(string num, int base) {
    string result;
    while (!num.empty()) {
        int remainder = 0;
        string quotient;
        for (char c : num) {
            int current = remainder * 10 + (c - '0');
            quotient.push_back(current / base + '0');
            remainder = current % base;
        }
        result.push_back(remainder + '0');
        // 去除前导零
        size_t pos = quotient.find_first_not_of('0');
        num = (pos == string::npos) ? "" : quotient.substr(pos);
    }
    reverse(result.begin(), result.end());
    return result;
}

---

五、练习题

1. 题目：输入一个十六进制数，输出其二进制表示。
   输入示例：1A3
   输出示例：000110100011

2. 题目：将十进制数 255 转换为八进制和十六进制。
   答案：八进制 377，十六进制 FF。

3. 题目：实现一个函数，判断二进制字符串是否为回文。
   参考代码：

   bool isBinaryPalindrome(string bin) {
       int left = 0, right = bin.size() - 1;
       while (left < right) {
           if (bin[left] != bin[right]) return false;
           left++;
           right--;
       }
       return true;
   }
   

---

掌握以上内容后，您将能轻松应对 CSP-J 中涉及进制转换的各类题目！ 🚀